当年逃的课,终究有一天要补回来。
——沃·兹寄·烁德
写一下主要是为了复习数学。
推导过程
在写ray marching的体渲染的时候学到了采样相位函数,PBR书里直接给出了一个和HG相位函数(Henyey-Greenstein Phase Function)对
在进行下文之前先回顾一下标准的HG相位函数吧:
虽然说直接抄也不是不可以,而且我看东西也比较囫囵吞枣,但是这个东西感觉还是有必要弄懂的。毕竟原本打算是用Schlick相位函数的。
搜了一下之后发现了Tiziano Binzoni的一篇论文The use of the Henyey–Greenstein phase function in Monte Carlo simulations in biomedical optics,里面大概就讲了这个事情。
主要原理还是对分布函数求逆就是均匀分布到原随机变量的函数。
里面作者提到原始的HG相位函数积出来后并没有数值解。但是可以把函数变形成以
询问了某位可爱的群友并经受一番嘲讽过后,大概是搞懂了这个变形的过程。
首先我们需要清楚相位函数是在球面上的概率密度函数,因此满足:
这样一来获得了累计分布函数就能很轻易的求解出逆分布函数了
设
顺便在这里对Schlick相位函数求一下采样的分布吧
还有一件事
最后绘制了一下得到了两个函数的图像,发现这两个函数在定义域内是接近对称而不是重合的。
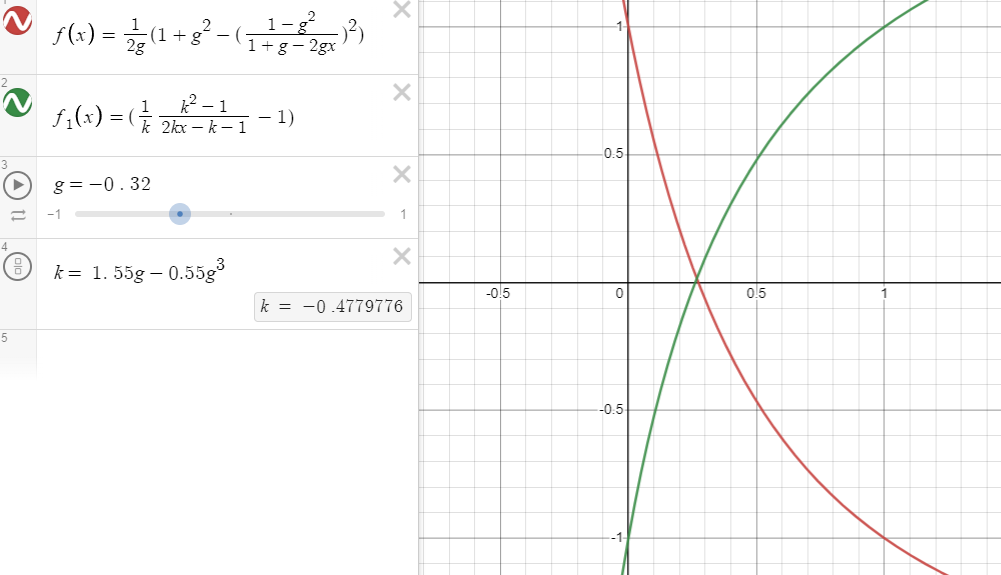
是在计算的时候做错了什么吗?并不是。注意到采样函数的结果值是
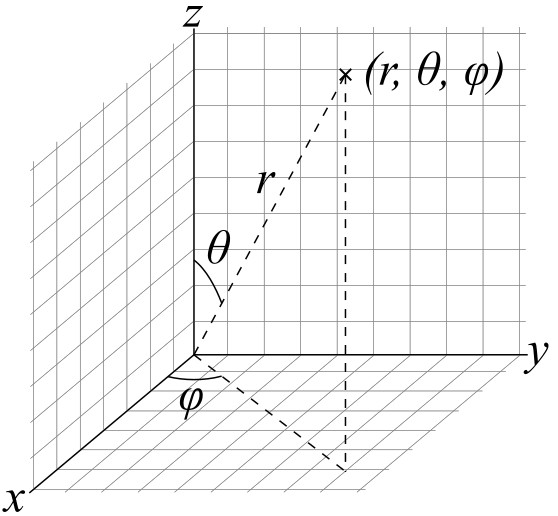
参考资料
- Binzoni, Tiziano & Leung, Terence & Gandjbakhche, Amir & Rüfenacht, Daniel & Delpy, D. (2006). The use of the Henyey-Greenstein phase function in Monte Carlo simulations in biomedical optics. Physics in medicine and biology. 51. N313-22. 10.1088/0031-9155/51/17/N04.
- Pharr, M., Jakob, W., & Humphreys, G. (2018). Physically based rendering: From theory to implementation. Morgan Kaufmann.